Simplifying Bonds: Pricing & Interest Rates

Chris A. Matlock, CPA, CFA, Chief Investment Officer

Bonds can be a daunting subject. You see their prices changing and yields varying, but how does all that work? What happens to bond prices as interest rates change? This article will attempt to provide investors with a better understanding of the relationship among market interest rates, bond prices and yield to maturity (YTM) of bonds. Before moving on, let’s provide some definitions for various aspects of bonds:

• Bond Price: The current market price of a bond available for sale in the market
• Par Value: The price a bond investor receives at the time of maturity, usually $1,000; Sometimes referred to as “Face Value”
• Coupon Rate: The stated interest rate paid by a bond when it was originally issued, usually fixed for the duration of the bond’s life
• Current Yield: This is the bond’s coupon divided by the current bond price
• Maturity: The length of time in years before a bond reaches its maturity date
• Yield to Maturity (YTM): The percentage rate of return for a bond at any given time assuming that the investor holds the bond to its maturity date. Considers current bond price, coupon rate and the time to maturity (at par value)

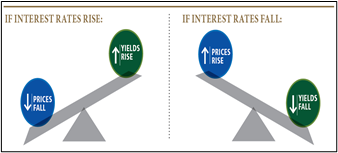A fundamental principal of bond investing is that market interest rates and bond prices move in opposite directions. This can be seen in the chart below. But why is that? Let us attempt to explain it by illustrating a couple of examples. In both examples, we start with the purchase of a newly issued 10-year maturity bond at par value of $1,000 with a 3% coupon which matches the current market interest rate of 3%.

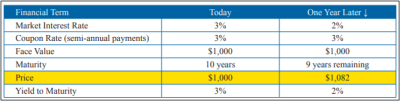
In Example 1, after the first year market interest rates decrease from 3% to 2%. In that instance, our 3% bond suddenly looks very attractive to other bond investors, who would then be    willing to pay more than par value for our bond so that it would then deliver a 2% market yield to the new investor over the remaining life of the bond. This would cause the bond price to increase to $1,082, or an 8.2% increase in price (we will spare you the math involved here!). The bond would now be trading at a “premium” to the $1,000 par value.

Example 1

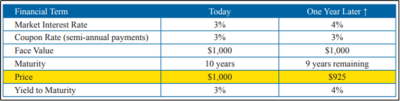
Conversely, in Example 2, market interest rates increase from 3% to 4% after the first year. In that instance, our 3% bond is now not as attractive to other bond investors, who would have to offer a lower price in order that it would then deliver to them a 4% market yield over the remaining life of the bond. This would cause the bond price to decrease to $925, or a 7.5% decrease in price, and the bond would now trade at a “discount” to par value. So, as you can now see, bond prices will adjust inversely to changes in interest rates.

Example 2

In the above examples, the bond we had purchased at par subsequently traded at either a premium or discount to its par value after the first year. This is actually the normal state of   affairs for bonds almost immediately after they are originally issued (at par), due to the fact that interest rates change daily. Since we rarely buy bonds at their issuance when they sell for par value, we usually buy them at a premium or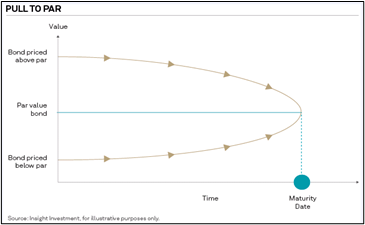 discount to par value depending on current market rates and the bond’s stated coupon. In the instance of  buying a bond at a premium, we would incur a loss on the bond upon maturity, receiving par   value then. But, of course, over the remaining life of that bond, we would have received a coupon rate that was above market interest rates at the time of purchase. Conversely, we might buy a bond with a coupon below prevailing  market interest rates at the time of purchase, and therefore pay a discount to par value for the bond. In this instance, we would recognize a gain on the bond at maturity when we receive the higher par value at that time, offsetting the lower than market coupon rate that we received prior to maturity. This certainty of a “Pull to Par” value can be seen in the previous chart, which shows how the price of a bond trading at a premium or discount degrades or accretes to par value over time to its maturity.

At the time of a bond purchase, a few things are known with certainty: 1) the investor will receive the stated coupon interest rate over the life of the bond; 2) They will receive par value upon the bond’s maturity; and 3) They will lock in a certain, calculated YTM for the remaining life of the bond assuming that it is held to maturity. In an environment like today’s where interest rates have risen rather dramatically, a bond investor will likely see unrealized losses in their portfolio. But those unrealized losses will slowly disappear as the bond accretes up to par value over its remaining life, assuming it is held to maturity.

Ultimately, the YTM at the time of a bond’s purchase is the true measure of expected return for that bond investment, regardless of up or down price movements due to inevitable changes in interest rates over the term of holding it. We believe the best way to manage that interest rate risk is by “laddering” a bond portfolio. By this, we mean constructing a bond portfolio where some of the bonds mature every year over a 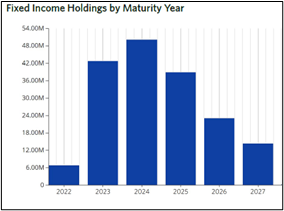select number of years. In the accompanying chart, we show a recent Goodman Financial Corp. aggregate composite bond ladder that is fairly representative of most client portfolios. You can see that this ladder extends no further out than 2027, with maturities in each of the intervening years and skewed to the earlier years in the ladder. So, while we might have had to lock in lower YTM’s for bonds purchased over the past couple of years than we would have liked, we will have the opportunity to reinvest those bonds as they mature each year at higher interest rates, assuming the rising interest environment we are currently experiencing continues to hold or rise even further.